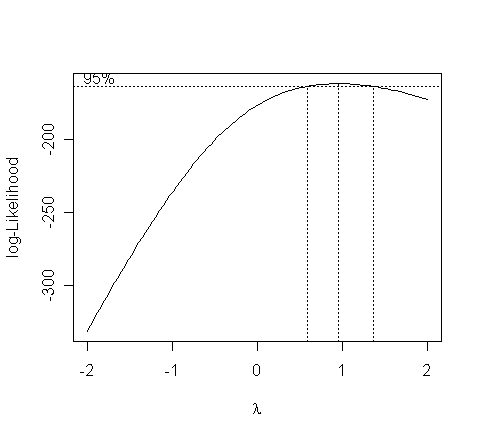
Does the response in the savings data need transformation? You'll need a function from the "MASS" library for performing Box-Cox transformation. Read in the library:
> library(MASS)
Try it out on the savings dataset:
> savings <- read.table("savings.data")
> g <- lm(sav ~ p15 + p75 + inc + gro,
data=savings)
> boxcox(g, plotit=T)

> boxcox(g, plotit=T, lambda=seq(0.5,1.5,by=0.1))
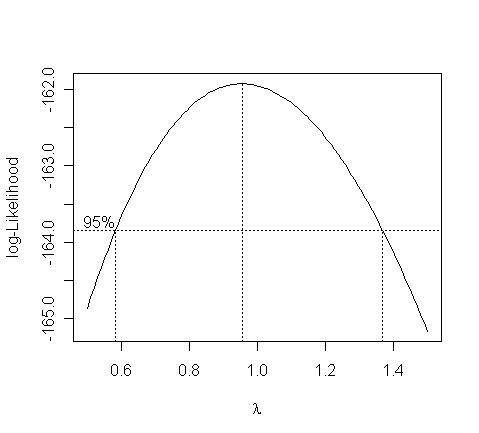
The confidence interval for lambda is from 0.6 to about 1.4. What do we conclude?
We can see that there is no good reason to transform.
Now consider the Galapagos data analyzed earlier:
> gala <- read.table("gala.data")
> gg <- lm(Species~Area+Elevation+Nearest+Scruz+Adjacent, data=gala)
> boxcox(gg, plotit=T)
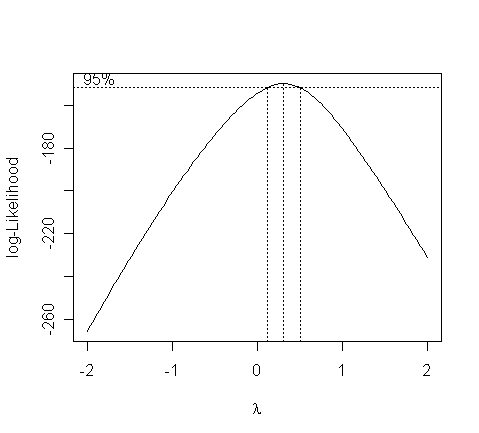
> boxcox(gg, lambda=seq(0.0,1.0,by=0.05), plotit=T)
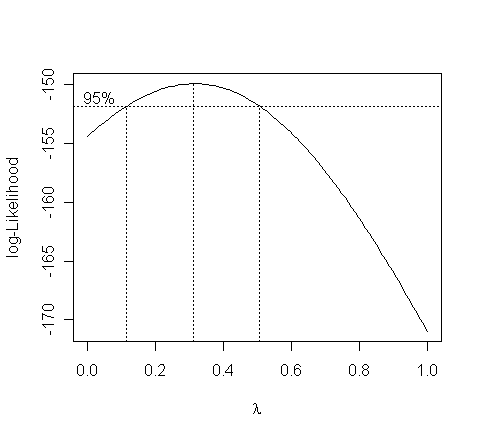
The confidence interval for lambda is from 0.1 to about 0.5. What do we conclude?
We see that perhaps a cube-root transformation might be best here.
A square root is also a possibility as this falls just within the confidence intervals. Certainly there is a strong need to transform.
¡@
Let's see if the gro variable in the savings dataset needs transformation:
> g <- lm(sav ~ p15 + p75 + gro + inc,
data=savings)
> g2 <- update(g, . ~ . + I(gro*log(gro))) # Add
gro*log(gro) to the model
> summary(g2)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)
23.7631766 8.6192503 2.757 0.00846 **
p15
-0.4026101 0.1545631 -2.605 0.01249 *
p75
-1.3604915 1.1258041 -1.208 0.23332
gro
1.6904514 1.2190155 1.387 0.17251
inc
-0.0004147 0.0009326 -0.445 0.65874
I(gro * log(gro)) -0.4675886 0.4392646 -1.064 0.29292
---
Residual standard error: 3.797 on 44
degrees of freedom
Multiple R-Squared: 0.3551, Adjusted R-squared:
0.2818
F-statistic: 4.845 on 5 and 44 DF, p-value: 0.001291
Examine the coefficient of gro*log(gro) - what should we conclude?
Now see if p15 should be transformed.
> g3 <- update(g, . ~ . + I(p15*log(p15))) ; summary(g3)
Compare the results of this test to the partial residual plot for p15.