Ordinal Multinomial Responses (Reading: Faraway (2006), section 5.3)

Returning to the nes96 dataset, suppose we assume that Independents fall somewhere between Democrat and Republican. We would then have an ordered multinomial response.

Proportional Odds Model.

We can fit a proportional odds model using the polr function from the MASS library:

> library(MASS)
> pomod <- polr(sPID ~ age + educ + nincome, nes96)
The deviance and number of parameter for this model are:

> c(deviance(pomod),pomod$edf)

which can be compared to the corresponding multinomial logit model:

> c(deviance(mmod),mmod$edf)

We see that:

• the proportional odds model uses fewer parameters because it assumes the predictors have a uniform effect on the 3 response categories (which saves (1+6+1)´(2-1)=8 parameters)

• but, the former does not fit quite as well as the latter

• typically, the output from the proportional odds model is easier to interpret

We may use an AIC-based model selection method to identify important predictors:
> pomodi <- step(pomod)

Thus, we finish with a model including just income as we did with the earlier multinomial model.

We could also use a likelihood-ratio test (i.e., difference-in-deviance test) to compare the model:

> deviance(pomodi)-deviance(pomod)

> pchisq(11.15136, pomod$edf-pomodi$edf, lower=F)

We see that the simplification to just income is justifiable.

We can check the proportional odds assumption by computing the observed (sample) odds proportions with respect to the predictor, which is income in this case. We have computed the log-odds difference between the cumulative probabilities g₁ and g₂:

> pim <- prop.table(table(nincome,sPID),1)
> pim

> logit <- function(p){log(p/(1-p))}

> logit(pim[,1])-logit(pim[,1]+pim[,2])

We see that:

• it is questionable whether these can be considered sufficiently constant

• but, at least there is no clear trend (exercise: check this point by yourself)

Now, let us consider the interpretation of the fitted coefficients:

> summary(pomodi)

We see that:

• the odds of moving from Democrat to Independent/Republican category (or from Democrat/Independent to Republican) increase by a factor of:

  > exp(0.0131199)

  [1] 1.013206

  as income increases by one unit ($1000)

• the intercept terms correspond to the b_0j in the lecture notes. So, for an income of $0, the predicted probability of being a Democrat is:

  > ilogit <- function(z) {exp(z)/(1+exp(z))}

  > ilogit(0.2091)

  [1] 0.5520854

  while that of being an Independent is:

  > ilogit(1.2915)-ilogit(0.2091)

  [1] 0.2323156

• we can compute predicted values for some income groups:

  > il <- c(8,26,42,58,74,90,107)

  > predict(pomodi,data.frame(nincome=il,row.names=il),type="probs")

       Democrat Independent Republican

  8   0.5260176   0.2401104  0.2338720

  26  0.4670494   0.2541497  0.2788009

  42  0.4153451   0.2617599  0.3228950

  58  0.3654398   0.2641787  0.3703815

  74  0.3182667   0.2612189  0.4205144

  90  0.2745483   0.2531094  0.4723423

  107 0.2324184   0.2395374  0.5280442

  Notice that:

  • the probability of being a Democrat uniformly decreases with income while that for being a Republican uniformly increases as income increases

  • the middle category of Independent increases then decreases (exercise: compare with the predicted values of the earlier multinomial logit model and explain why they are different)

  • the type of behavior can be expected from the latent variable representation of the model.

  • we can illustrate the latent variable interpretation of proportional odds by computing the cut-points for incomes of $0, $50,000, and $100,000:

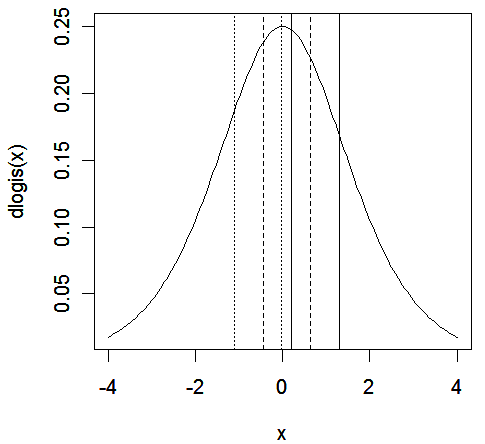
  > x <- seq(-4, 4, by=0.05)
  > plot(x,dlogis(x),type="l")
  > abline(v=c(0.2091, 1.2915))
  > abline(v=c(0.2091, 1.2915)-50*0.0131199, lty=2)
  > abline(v=c(0.2091, 1.2915)-100*0.0131199, lty=5)

  

  We see that:

  • the solid lines represent an income of $0, dotted lines are for $50,000, and dashed lines are for $100,000

  • probability of being a Democrat is given by the area lying to the left of the leftmost of each pair of lines

  • probability of being a Republican is given by the area to the right of the rightmost of the pair

  • probability of being a Independent are represented by the area in between

Ordered Probit Model.

Applying the ordered probit model to the nes96 data, we find:

> opmod <- polr(sPID ~ nincome, method="probit")
> summary(opmod)

Notice that:

• this deviance is similar to the deviance in the proportion odds model (logit version of this model)

• but, the coefficients appear to be different

• however, if we compute the same predictions:

  > dems <- pnorm(0.1284-il*0.008182108)
  > demind <- pnorm(0.7976-il*0.008182108)
  > cbind(dems, demind-dems, 1-demind)

            dems                   

  [1,] 0.5250941 0.2428653 0.2320406

  [2,] 0.4663951 0.2542857 0.2793192

  [3,] 0.4147868 0.2602813 0.3249319

  [4,] 0.3646104 0.2620563 0.3733333

  [5,] 0.3166540 0.2595235 0.4238225

  [6,] 0.2715971 0.2528070 0.4755959

  [7,] 0.2275060 0.2414536 0.5310405

  We see that the predicted values are very similar to those seen for the logit

• actually, if the coefficients are appropriately rescaled, they can be also very similar

Proportional Hazards Model.

The extreme value distribution is not symmetric like the logistic and normal distribution. So, there seems little justification for applying it to the nes96 data. But, the command is:

> summary(polr(sPID ~ nincome, method="cloglog"))