Generalized least square (Reading: Faraway(2005, 1st edition), 6.1)

We'll use a built-in R dataset called Longley's regression data where

• the response is number of people employed, yearly from 1947 to 1962, and

• the predictors are

  • GNP implicit price deflator (1954=100),

  • GNP,

  • unemployed,

  • armed forces,

  • non-institutionalized population 14 years of age and over, and

  • year.

• The Longley data was collected over 16 years and it is reasonable to expect that there might be some correlation between errors in successive years. 

Let us take a look of some background knowledge of the data set.

> help(longley) 

> data(longley) # load the data into R

> longley # take a look of the data

> emp <- longley[,7] # extract the Employed variable
> gnp <- longley[,2] # extract the GNP variable
> pop <- longley[,5] # extract the Population variable

Let's fit a model with

• number of people employed as the response and

• GNP and Population as the predictors.

> g <- lm(emp~gnp+pop) # fit the model
> summary(g,cor=T) # summary of the fitted model

Note that

• the model is built under the assumption that the errors are uncorrelated.

• Check the correlation between the estimates of predictors gnp and pop. What do you notice? 

  > cor(gnp, pop) # correlation between two predictors

  [1] 0.99109

  • Compare it to the correlation of coefficient. Note that one is positive and another is negative. Explain why.

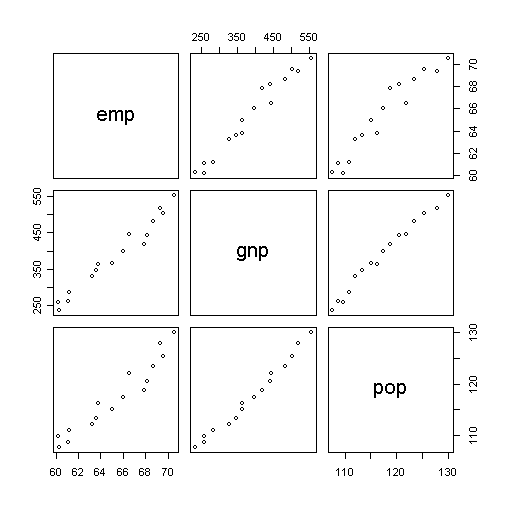
  • Now, let's take a look of their scatter plots.

    > pairs(cbind(emp,gnp,pop)) # draw pairwise scatter plots

    

    What have you found from the plots?

Notice that

• In data collected over time such as this, successive errors could be correlated.

• Suppose we assume that

  • cor(ε_t, ε_t+1)=0.5

  • all other off-diagonal elements are zero

  • (Note: in practice, we would want to assign a model to ε_t's, not only to state the form of correlation).

We will calculate the results with correlated errors "by hand" below and compare them to those assuming uncorrelated errors.

> x <- cbind(rep(1,16),gnp,pop) # extract the X-matrix
> Sig <- diag(16) # start to construct the Σ matrix
> Sig # diagonal entries in the correlation matrix are always one

> Sig[abs(row(Sig)-col(Sig))==1] <- 0.5 # assign the off-diagonal values of Σ
> Sig # the Σ matrix as we want it

> Sigi <- solve(Sig) # the Σ^-1
> xtxi <- solve(t(x) %*% Sigi %*% x) # calculate(X^TΣ^-1X)^-1
> beta <- xtxi %*% t(x) %*% Sigi %*% emp # β-hat = (X^TΣ^-1X)^-1X^TΣ^-1Y
> beta # the GLS estimate of β

• Let us see how it compares to the previous result

  > g$coef

  (Intercept)         gnp         pop

  88.93879831  0.06317244 -0.40974292

> res <- emp-(x%*%beta) # the residuals for this fit
> sig <- sqrt((t(res) %*% Sigi %*% res)/g$df) # σ-hat is estimated

> sig # the value of σ-hat

• Note that you cannot use "sqrt(sum(res^2)/g$df)" to calculate the σ-hat. Why?

• Let us see how it compares to the previous result

> sqrt(diag(xtxi))*sig # s.e.(β-hat_i)=sqrt((X^TΣ^-1X)^-1_ii)*(σ-hat), the standard errors for β-hat allowing for the correlation

• Let us see how it compares to the previous result

The simplest way to model the correlation between successive errors is the autoregressive (AR) form:

ε_t+1 = ρε_t + δ_t, where δ_t~N(0,τ²).

A rough estimate of the correlation ρ  is:

> cor(g$res[-1], g$res[-16]) # calculate cor(ε_t, ε_t+1)

Under the AR(1) assumption,

• Σ_ij=ρ^|i-j|.

• for simplicity, lets assume we know that ρ=0.31041.

We now construct the Σ matrix and compute the GLS estimate of β along with its standard errors.
> Sigma <- diag(16) # start to calculate Σ
> Sigma <- 0.31041^abs(row(Sigma)-col(Sigma)) # assign the off-diagonal values of Σ
> print(Sigma, digits=1) # take a look of Σ

• Please try to calculate the GLS estimates and their s.e.'s, residuals, and σ-hat "by hand" as shown above by yourself.

We will try another way, regressing S^-1y on S^-1x, to get the results:

> sm <- chol(Sigma) # calculate S^T, where Σ=SS^T. the "chol" command compute the Choleski factorization
> smi <- solve(t(sm)) # calculate S^-1
> sx <- smi %*% x # calculate S^-1x
> sy <- smi %*% emp # calculate S^-1y
> g2 <- lm(sy~sx-1) # regress S^-1y on S^-1x, remember to exclude the constant term

> summary(g2, cor=T) # take a look of the results

• Compare it to the results you calculated "by hand" and check whether they are identical.

• Q: Does the R-square still has the same explanation as in the case of ordinary least square?

  • Can you compare it to the R-square in model g and conclude that the g2 has a better fit than g?

  • Note that the R-square in g2 is obtained based on S^-1y and S^-1x, rather than y and x as in model g.

In practice,

• we would not know whether ρ  equals 0.31041.

• We'd need to estimate it from the data.

Our initial estimate is 0.31041, but once we fit our GLS model we'd need to re-estimate ρ  as:

> cor((t(sm)%*%g2$res)[-1], (t(sm)%*%g2$res)[-16]) # result using correct residuals, i.e., S*(residual)

• Note that you cannot do this using the residuals of g2 (Why?). Check it out:

  > cor(g2$res[-1], g2$res[-16]) # result using wrong residuals

  [1] 0.1395297

And then,

• compute the model again with ρ =0.3564162

• the process would be iterated until convergence

This is cumbersome.

A more convenient approach may be found in the "nlme" package, which contains a GLS fitting function. The approach is to

• model Σ and

• jointly estimate the regression parameters and parameters in Σ using a likelihood-based method.

We will use the approach to fit the model below (remember to add the "nlme" package if you haven't done it):

> library(nlme) # load the "nlme" package.

> help(gls) # take a look of the document of "gls" command. Pay some attention to the "correlation" option.
> year <- longley[,6] # extract the Year variable

Let us fit the model with correlated errors following an AR(1) structure.

> g3 <- gls(emp~gnp+pop, correlation=corAR1(form=~year)) # Use "help(corClasses)" and "help(corAR1)" to get more information about correlation structure.
> summary(g3) # take a look of the fitted model

We can see that

• the estimated value of ρ is 0.6441692

• however, if we check the confidence intervals for ρ:
  > intervals(g3) # calculate confidence intervals of parameters

  Approximate 95% confidence intervals

   

   Coefficients:

                    lower         est.       upper

  (Intercept) 71.18320461 101.85813306 132.5330615

  gnp          0.04915865   0.07207088   0.0949831

  pop         -0.88149053  -0.54851350  -0.2155365

  attr(,"label")

  [1] "Coefficients:"

   

   Correlation structure:

           lower      est.     upper

  Phi -0.4444668 0.6441692 0.9646106

  attr(,"label")

  [1] "Correlation structure:"

   

   Residual standard error:

      lower      est.     upper

  0.2474787 0.6892070 1.9193820

  • We see that ρ is not significantly different from zero because its confidence interval contains zero.