Fitting a Binomial GLM (Reading: Faraway (2006, 1st ed.), section 2.1~2.2)

    Here is a data set  from a study of rubber O-ring seals in the rocket boosters of space shuttle. Each shuttle had two booster, each with three O-rings. The data recorded the number of O-rings out of six showing some damage due to blow by and erosion in 23 previous shuttle missions. Because rubber becomes more brittle and is a less effective sealant at lower temperatures, we are interested in how the probability of failure in a given O-rings is related to the launch temperature. We start by reading the data into R.
> orings <- read.table("orings.txt")
　

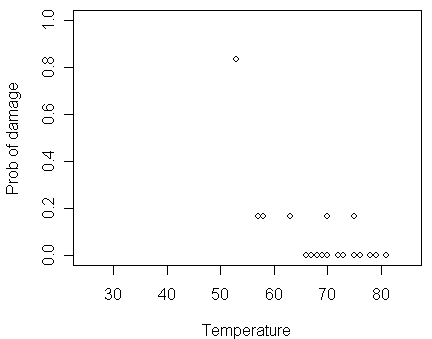
    We then take a look of the data and plot the proportion of damaged O-rings against temperature.

> orings

> plot(damage/6 ~ temp, orings, xlim=c(25,85), ylim = c(0,1), xlab="Temperature", ylab="Prob of damage")

The figure shows some tendency that the proportion of damage gets larger when the temperature decreases.

    To build a model, a naive approach based on Normal linear model simply fit a line to this data:

> lmod <- lm(damage/6 ~ temp, orings)
> summary(lmod)

> abline(lmod)

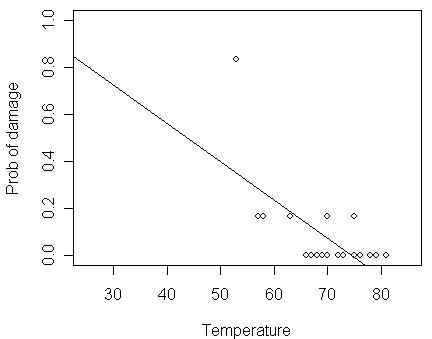
For this data set, there are several problems with this approach:

• Predicted probability may be > 1 or < 0

• For a binomial observation with only six trials, the Normal approximation for damage/6 is too much of a stretch

• The variance of a binomial variable is not constant which violate another crucial assumption of the Normal linear model

Although we could use transformation and weighting to correct some of these problems, it is better to develop a model that is directly suited for binomial data.

    We now use R to fit a binomial GLM for the data:

> logitmod <- glm(cbind(damage,6-damage) ~ temp, family=binomial, orings)
The important points to note for the command:

• For binomial response data, we need two pieces of information about the response values --- y_x (the number of "successes") and n_x (the number of trials). In R, one way of doing this is to form a two-column matrix with the 1st column representing y_x and the 2nd column n_x-y_x.

• We can specify the response is binomially distributed in the "family" option.

• The default choice of link function is the logit --- other choices need to be specifically stated as we shall see shortly.

Now, let us take a look of the fitted model:

> summary(logitmod)

We should notice that:

• The estimated GLM coefficients are given in the above output --- b₀-hat=11.66 and b₁-hat=-0.216 along with their respective standard errors 3.296 and 0.053.

• The "z-value" (i.e., Wald test) equals (b-hat)/[se(b-hat)], which is asymptotically distributed as N(b, 1). The p-value for testing b=0 is given in "Pr(>|z|)".

• The "Null deviance" is the deviance for a model with no predictors and just an intercept term (its degree of freedom equals k-1 where k is the number of covariate classes)

• The "Residual deviance" is the deviance for the current model (its degree of freedom equal k-p where p is the number of parameters in the current model)

    Let us compare the logit fit to the data:

> plot(damage/6 ~ temp, orings, xlim=c(25,85), ylim = c(0,1), xlab="Temperature", ylab="Prob of damage")
> x <- seq(25,85,1)
Here is a function writen by Prof. Faraway for calculating the inverse of logit transformation. You can copy & paste it to the R console window before executing next command.

> lines(x,ilogit(11.6630-0.2162*x))

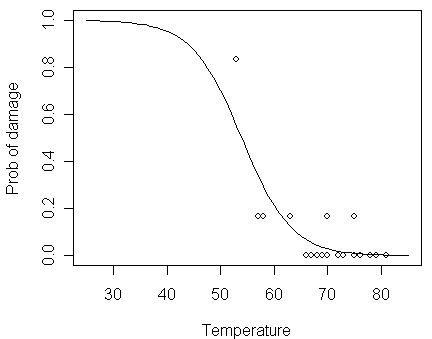
Please notice:

• how the fitted probability in the logit fit tends toward zero and one at high and low temperatures, respectively

• the fitted probability never actually reach 0 or 1, so the model never predicts anything to completely certain or completely impossible

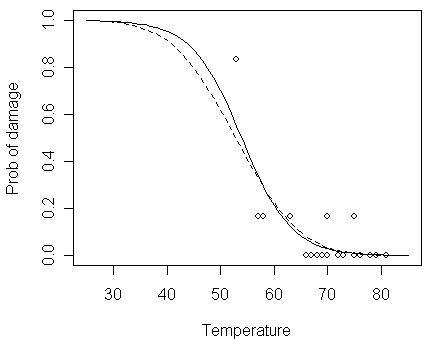
    Now, let us compare the logit fit to the probit fit:

> probitmod <- glm(cbind(damage,6-damage) ~ temp, family=binomial(link=probit), orings)
Compare this command with that for logit fit, and notice that how we assign the probit link function. Let us take a look of the fitted model under the probit link:

> summary(probitmod)

Notice that:

• the b₀-hat=5.59 and b₁-hat=-0.105 are quite different from those estimated in the logit fit (Q: should they be expected to have similar values?)

• although the coefficients seem quite different, the fits are similar (as can be seen in the figure below), particularly in the range of the data

> lines(x,pnorm(5.5915-0.1058*x),lty=2)

    In Jan 1986, the space shuttle Challenger exploded shortly after launch. At the time of the launch, the temperature was 31°F. We can predict the response at 31°F for both models:

> ilogit(11.6630-0.2162*31)

> pnorm(5.5915-0.1058*31)

We see a very high probability of damage with either model although we still need to develop some inferential techniques before we leap to conclusion.

Hypothesis testing in a Binomial GLM (Reading: Faraway (2006), section 2.3)

Provided that y_x is truly binomial and that n_x are relatively large, for a model with p parameters, the deviance D is approximately c² with degrees of freedom k-p if the model is correct. Thus, we can use D as a goodness-of-fit measure to test whether the logit model for O-ring data is an adequate fit:

> deviance(logitmod)

> df.residual(logitmod)

> pchisq(16.91228,21,lower=FALSE)

We see that:

• this p-value >> 0.05 Þ we may conclude that this model fits sufficiently well

• of course, this does not mean that this model is correct or that a simpler model might not also fit adequately

For the null model (i.e., the model with no predictors and only an intercept term), its deviance equals 38.898 with degrees of freedom 22. So, for the null model, the chi-square test for goodness-of-fit returns:
> pchisq(38.898,22,lower=FALSE)

Because the p-value < 0.05, we can see that the fit is inadequate.

    Note that a c² with degrees of freedom d has mean d and standard deviation sqrt(2d) so that it is often possible to quickly judge whether a deviance is larger or small without explicitly computing the p-value. If the deviance is far in excess of the degrees of freedom, the null hypothesis can be rejected.

    We can also use the deviance to compare two nested models S and L, where SÌL. To test H₀: S against H₁: L\S, the test statistics is D_S-D_L, which is asymptotically distributed as c² with degrees of freedom df_S-df_L assuming that the model S is correct (i.e., under null hypothesis H₀). For the O-ring data, we can use this to test the significance of temperature by computing the difference in the deviances between the models with and without temperature:

• the model without temperature (i.e., S) is just the null model

• the model with temperature (i.e., L) is the fitted model in the object logitmod

• D_S=38.898 and D_L=16.912

• df_S=22 and df_L=21

So, the p-value of the test is:

> pchisq(38.898-16.912,1,lower=FALSE)

Notice that:

• since the p-value is so small, we can conclude that the effect of launch temperature is statistically significant.

• the p-value does not equal the p-value of Wald test (=4.78e-05), although there is no practical difference in this particular example

    The deviance-based test can be applied to arbitrary nested models. However, when S is a model by removing only one parameter in L (i.e., H₀: b_i=0 for some i), an alternative test is the z-value (Wald test). In contrast to the Normal linear model, the two statistics do not generate identical p-values. For the reason of Hauck-Donner effect, the deviance-based test is usually preferred.

    For the accuracy of the asymptotical approximation, the test involving differences of deviances is generally more accurate than the goodness-of-fit test involving a single deviance (notice that the latter usually has a larger degrees of freedom than the former).

    To construct confidence interval for parameters, we can use the normal approximation for the parameter estimates (originated from Wald test). For example, a 95% confidence inter for the parameter of temperature in the logit model would be (1.96 is the critical value z^(0.05/2)):

> c(-0.21623-1.96*0.05318,-0.2162+1.96*0.05318)

Notice that the confidence interval does not contain zero, which is consistent with the z-value testing result.

    It is also possible to construct a profile likelihood-based confidence interval (c.f., deviance-based test).

• To do this, it is important to load the MASS package before using the confint command.

• Otherwise, the default confint method for ordinary linear model will be used, which will not be quite right.

• Before loading a package, you need to check whether the package has been added in R.

• In R, to add a new package, you can do it from the "程式套件"→"安裝程式套件" in the toolbar and choose a CRAN mirror which is close to you. Then, in the Packages window, double-click on the "MASS".

> library(MASS)
> confint(logitmod)

We can see that:

• the profile likelihood-based confidence interval is slightly different from the previous confidence interval in this case

• the profile likelihood-based confidence interval is more away from zero than the previous confidence interval,  which is consistent with the result that the deviance-based test has a smaller p-value than the Wald test in this case

• the profile likelihood-based method is generally preferable for the Hauck-Donner reason although it takes more work to compute

Although we have only computed results for the logit link, the same methods would apply for the probit or other link. You should at least practice the probit case by yourself.